Introduction
The binomial theorem is a quick way of expanding a binomial expression that is raised to some power. When the binomial expressions are expanded, is there any type of pattern developing which might help us expand more quickly? It is fun to investigate how it works out in a pattern.
Sample Question
Question 1
(a) Expand for
.
(b) What observations can we make about the terms in the expansion of ?
(c) Write down the general formula for the binomial expansion of .
(d) Obtain the general formula for binomial expansion of where
is a rational number, and state the condition for the validity of the binomial expansion with a negative integral exponent or a rational exponent.
Question 2
Deduce the value of
(a)
(b)
Question 3
The number may be defined by
. Determine the approximate value for
.
Sample Solution
Question 1 (a)
Question 1 (b)
- There are
terms in the expansion.
- The first term’s powers start at
and go down.
- The second term’s powers start at 0 and go up.
- The coefficients are from Pascal’s triangle or
.
Question 1 (c)
Question 1 (d)
Question 2
Question 3
Here are our most recent updates posts
- Feel free to check it out -
STPM 2021 Term 2 Exam Timetable
View the exam timetable for STPM 2021 Term 2. Countdown to STPM 2021 Examination. Join my tuition to help you achieve better results in the exam. Contact (60) 018-2016992 or kklee@kkleemaths.com for more information.
Integration of cos^3 x
There are many methods to integrate . 1. Use trigonometric identity Given that , -Here are our most recent updates posts- Feel free to...
STPM 2018 Term 3 Mathematics (T) Coursework Sample Answer
STPM 2018 term 3 mathematics (T) Coursework sample Guideline for solving STPM 2018 Term 3 Mathematics (T) PBS coursework assignment methodology Hint: Binomial Theorem Chi-Squared tests tabulate Thanks for helping in doing the survey. You can find...
STPM 2018 Term 2 Mathematics (T) Coursework Sample Solution
STPM 2018 term 2 mathematics (T) Coursework sample Guideline for solving STPM 2018 Term 2 Mathematics (T) PBS coursework assignment methodology Hint: limits L' Hopital rule Rationalisation Indeterminate Form Existance of limitsThanks the two students who sent me the...
Integration Booklet Page 10 Page 11 Solution
Here are our most recent updates posts- Feel free to check it out -
STPM 2018 Term 1 Mathematics (T) Coursework Sample
Question A complex number is an extension of a real number and it can be represented in Cartesian and polar forms. In this assignment, you are required to explore the powers and roots of complex numbers. 1 (a) Let z =1+i. Find z^n, where n = 2, 3, 4, …, and represent...





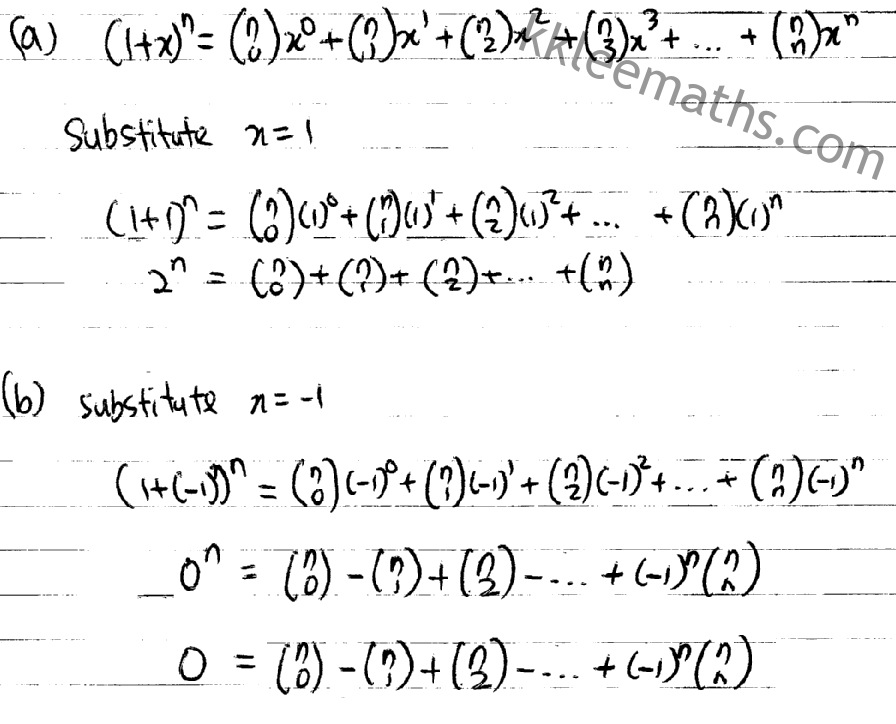










THX…
Sir, can u explain question 2
To get the equation, you need to substitute x=1 and x=-1
hi, may i know how to write the methodology? i have no idea. QAQ
For methodology, try to write about the methods/theorem/ways you used to solve the questions.
sir, may i know how to write about “communication”? and what is “viva”
It depends on your teacher.
How about term 2 methodology?
Hi. Are you referring to Mathematics (M)? I havent receive the question paper. T.T