Back to Blog

Read Article

Discussion –

Read Article

Discussion –

STPM PBS Assignment

STPM 2017 Mathematics (M) Term 1 Assignment

By KK LEE

July 6, 2016

STPM 2017 Term 1 MM Coursework Explained.

—00

The lower sum and upper sum are defined as follows: Lower Sum =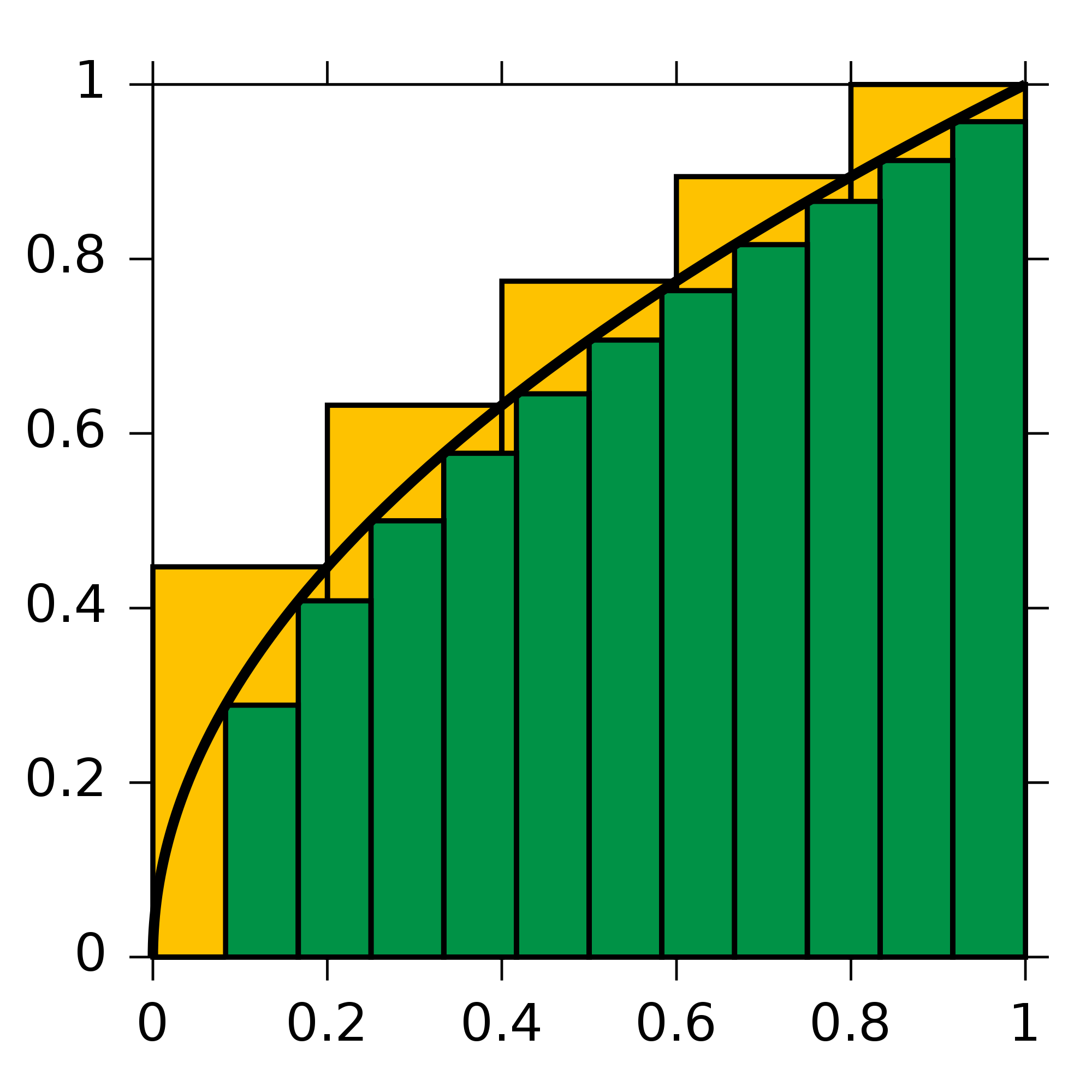 $\sum_{i=1}^n f(m_i)\triangle x$ Lower Sum = $\sum_{i=1}^n f(M_i)\triangle x$ You are required to investigate the area of the region bounded by the curve $y=f(x)=x^2+1$ , the x-axis, and the lines x=0 and x=2.

“Only sample solution for mathematical part will be posted. Please ask your school teacher for introduction, methodology, and conclusion.”

—01

(a) (i) Sketch the curve with 5 inscribed rectangles and evaluate the lower sum. (ii) Sketch the curve with 5 circumscribed rectangles and evaluate the upper sum. (iii) Comment on your results. (b) (i) Tabulate the lower sums and upper sums for n=10, 20, 40. (ii) What do you observe about the lower sums and upper sums as n increases?

—02

Let $A_n=\sum_{i=1}^n f(c_i)\triangle x$ . (a) (i) Show that $A_n=\frac{4}{3}\left[\frac{(n+1)(2n+1)}{n^2}\right]+2$ if $c_i=a+i\triangle x$ , (ii) Tabulate the values of $A_i$ for n=1000, 5000, 10000, 50000, 100000, 500000. (iii) Evaluate $\lim_{n\to \infty}A_n$ . (b) It is given that $A_n=\frac{4}{3}\left[\frac{(n-1)(2n-1)}{n^2}\right]+2$ if $c_i=a+(i-1)\triangle x$ . Repeat steps (a)(ii) and (a)(iii). (c) What happens to the value of $\lim_{n\to\infty} A_n$ if $a+(i-1)\triangle x < c_i < a+i\triangle x$ ?

—03

(a) Use the Fundamental Theorem of Calculus to evaluate $\int_0^2 f(x) dx$ . (b) Suggest a definition of a definite integral.

“Scroll down for the sample solution!”

1 (a) (i)

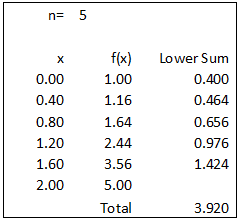
Lower sum can be calculated by calculate the total area of the inscribed rectangles (refer the diagram). For n=5, △ x=2/n=2/5=0.4. Area of rectangle is given by f(x) multiply △ x or f(x) multiply 0.4.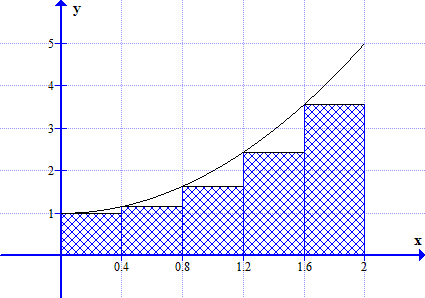

1 (a) (ii)

Lower sum can be calculated by calculate the total area of the circumscribed rectangles (refer the diagram). For n=5, △ x=2/n=2/5=0.4. Area of rectangle is given by f(x) multiply △ x or f(x) multiply 0.4.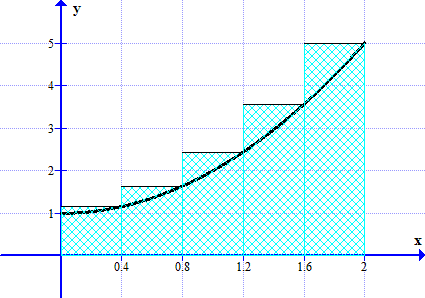

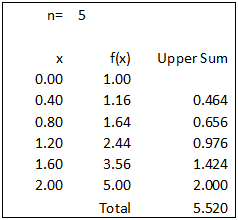
1 (a) (iii)

The upper sum is 40.8% larger than the lower sum. The exact area should be between 5.520 and 3.920.

1 (b) (i)

For n=10, △ x=2/n=2/10=0.2. Area of rectangle is given by f(x) multiply △ x or f(x) multiply 0.2.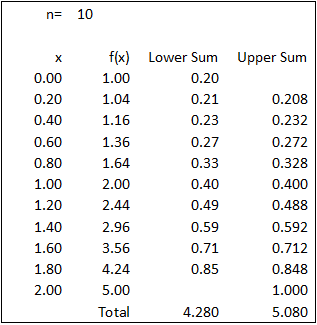

1 (b) (i)

For n=20, △ x=2/n=2/20=0.1. Area of rectangle is given by f(x) multiply △ x or f(x) multiply 0.1.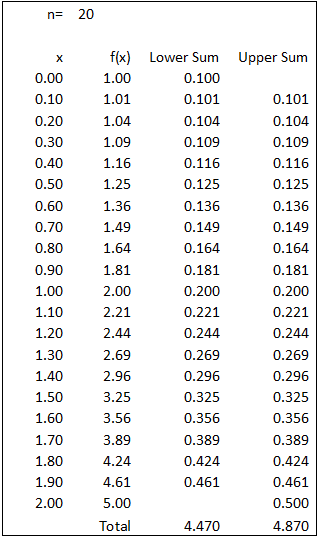

1 (b) (i)

For n=40, △ x=2/n=2/40=0.05. Area of rectangle is given by f(x) multiply △ x or f(x) multiply 0.05.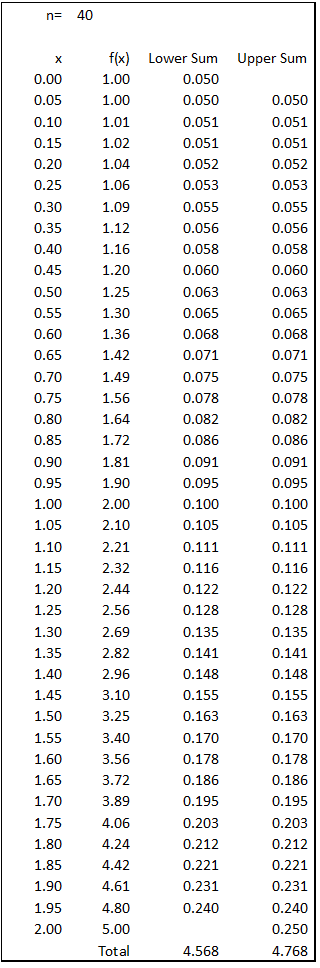

1 (b) (ii)

As n increases the gap between the lower sum and upper sum is getting smaller.

2 (a) (i)

You need to find the proof for the sum $\sum_{i=1}^n r^2=\frac{n(n+1)(2n+1)}{6}$ .

2 (a) (ii)

Prepare the table using the formula provided in part (i)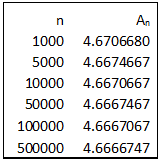

2 (a) (iii)

Find the limit.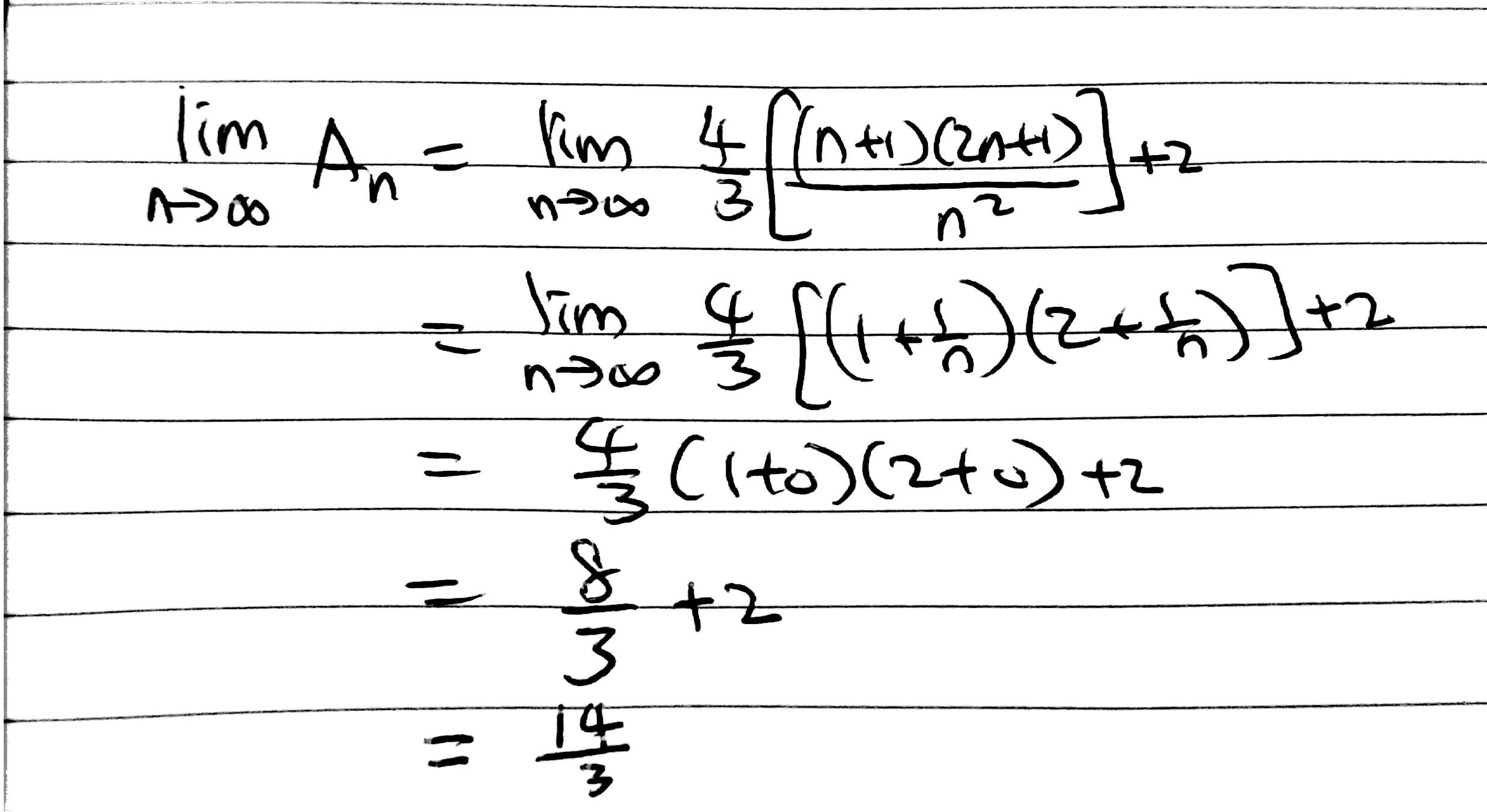

2 (b) (ii)

Prepare the table using the formula provided in part (i)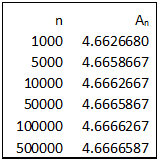

2 (b) (iii)

Find the limit.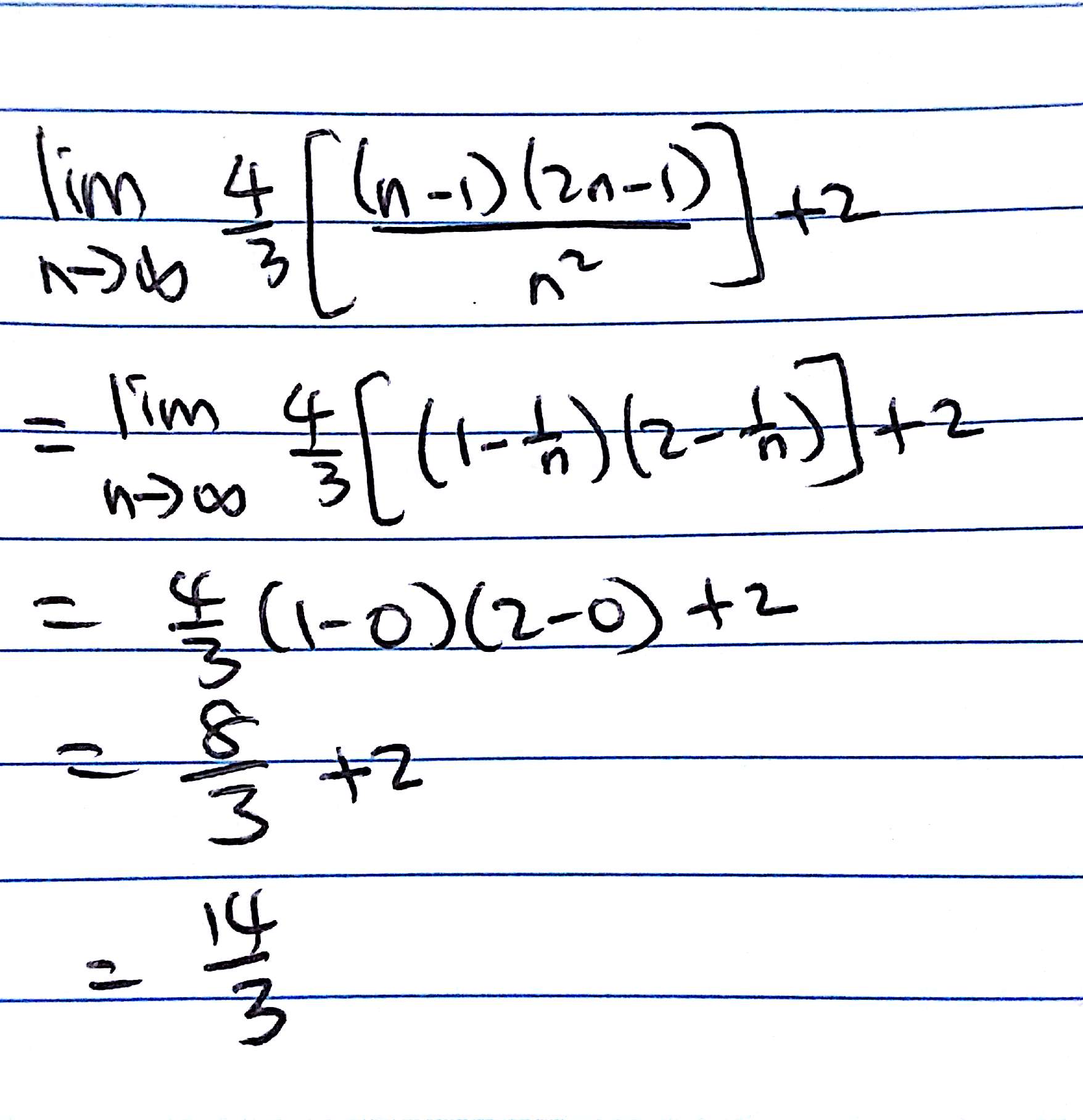

2 (c)

Same value.

3 (a)

Normal integration.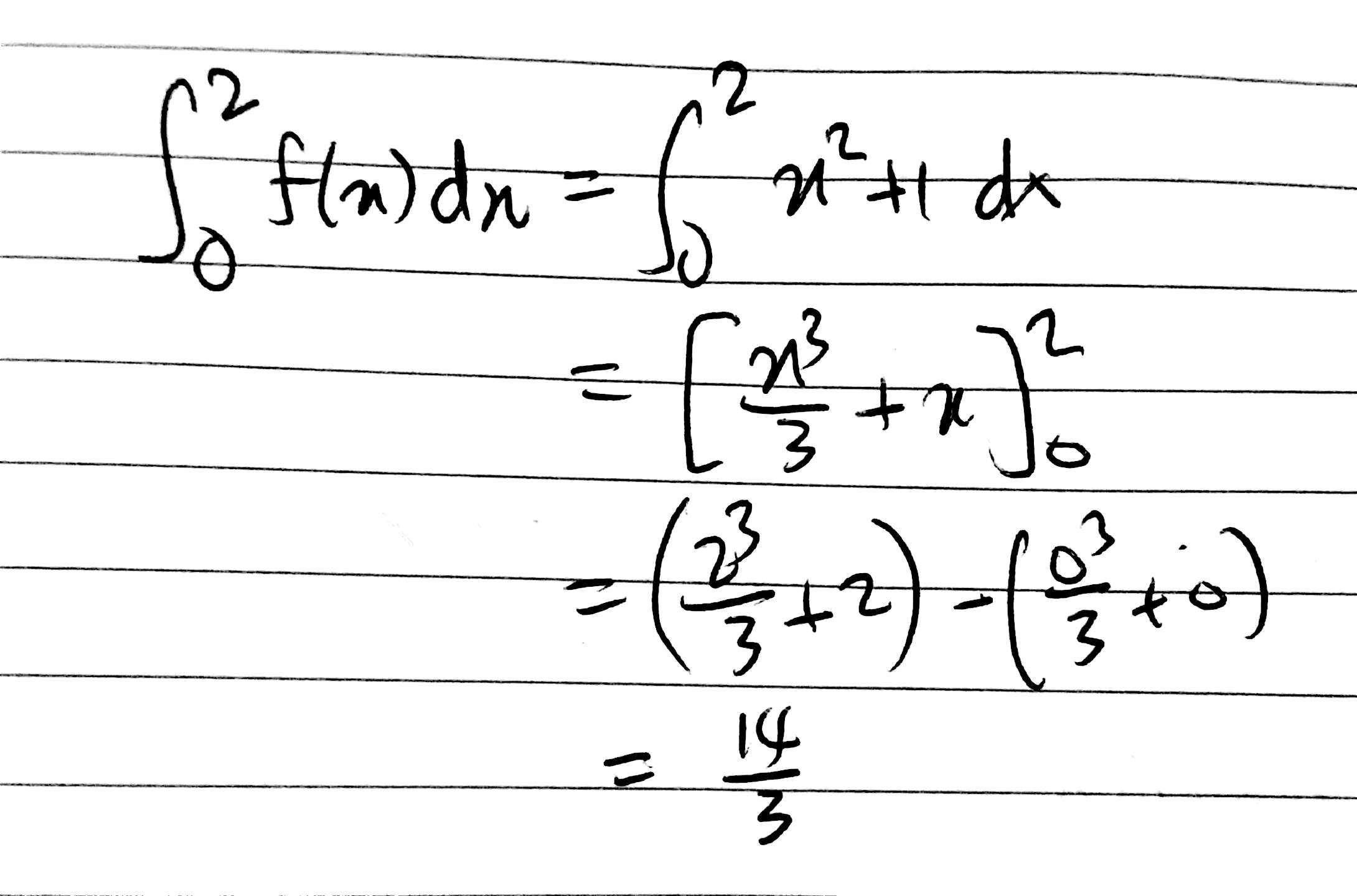

Here are our most recent updates posts

- Feel free to check it out -

STPM 2021 Term 2 Exam Timetable

STPM Exam

View the exam timetable for STPM 2021 Term 2. Countdown to STPM 2021 Examination. Join my tuition to help you achieve better results in the exam. Contact (60) 018-2016992 or kklee@kkleemaths.com for more information.

Integration of cos^3 x

Random Question

There are many methods to integrate . 1. Use trigonometric identity Given that , -Here are our most recent updates posts- Feel free to...

STPM 2018 Term 3 Mathematics (T) Coursework Sample Answer

STPM Coursework

STPM 2018 term 3 mathematics (T) Coursework sample Guideline for solving STPM 2018 Term 3 Mathematics (T) PBS coursework assignment methodology Hint: Binomial Theorem Chi-Squared tests tabulate Thanks for helping in doing the survey. You can find...

STPM 2018 Term 2 Mathematics (T) Coursework Sample Solution

STPM Coursework

STPM 2018 term 2 mathematics (T) Coursework sample Guideline for solving STPM 2018 Term 2 Mathematics (T) PBS coursework assignment methodology Hint: limits L' Hopital rule Rationalisation Indeterminate Form Existance of limitsThanks the two students who sent me the...

Integration Booklet Page 10 Page 11 Solution

KK LEE Booklet Solution

Here are our most recent updates posts- Feel free to check it out -

STPM 2018 Term 1 Mathematics (T) Coursework Sample

STPM Coursework

Question A complex number is an extension of a real number and it can be represented in Cartesian and polar forms. In this assignment, you are required to explore the powers and roots of complex numbers. 1 (a) Let z =1+i. Find z^n, where n = 2, 3, 4, …, and represent...

Tags: Differentiation Integration MM Term 1 STPM 2017 STPM MM

← Previous Post Next Post →

KK LEE

KK LEE has been a STPM Mathematics tuition teacher since June 2006, but his love of Maths dates back to at least 1999 when he was Form 4. KK LEE started teaching in 2006 at Pusat Tuisyen Kasturi. He was known as "LK" when he was teaching in PTK. After teaching STPM Mathematics for 8 years in PTK, he joined Ai Tuition Centre in 2014. Over the years he has taught Mathematics (T), Mathematics (S), Mathematics (M), Additional Mathematics.

46 Comments

Ke ying on July 7, 2016 at 3:06 pm

how to find f(mi) and the lower sum ?
and the comment for my results how to write?
Reply
- KK LEE on July 7, 2016 at 3:11 pm
  
  Sample solution will be posted once they are available or after i discuss the solution in class.
- Ke ying on July 7, 2016 at 3:15 pm
  
  okay,thanks
- yin on December 6, 2017 at 4:56 pm
  
  may i kw u gt 2018 sem 1 assignment answer
- KK LEE on December 8, 2017 at 1:37 am
  
  No. I din write it.
Aries Christie Lawrence on July 9, 2016 at 11:58 pm

Hi. I’m Aries. I’m not your student. But I really need explanation. Because I’m so confused and I really dont know how to start my coursework. I hope that you can help me out. Thanks Sir.
Reply
- KK LEE on July 10, 2016 at 12:26 am
  
  Hi. If you read properly. I have mentioned there. I will post the solution asap when they are available. I will write it after my holiday. 🙂
- ywlai on July 29, 2016 at 8:46 pm
  
  Aries Christie Lawrence , do you mind to send me a sample of introduction? or anyone here can share v me? thanks and appreciate a lot
- student on August 3, 2016 at 10:49 pm
  
  @ywlai how you do your introduction ? what are the important point need to mentions ? Can you share with me ? thank you
- amirtha on November 7, 2016 at 8:33 pm
  
  I’ve difficult to understand the project question sir, can you briefly explain what i should do from beginning coz my tutor left hand and ask me to do own. I was worried coz still left several day to past my assigment.
- KK LEE on November 8, 2016 at 12:55 am
  
  Hi. Try to get help from other teacher from your school. I will only help on the maths part.
Aries Christie Lawrence on July 10, 2016 at 1:25 am

Ok.thanks sir.?
Reply
Nur on July 30, 2016 at 6:14 pm

Hi sir..our school just startd our coursework..but I’m still confuse on finding the lower sum and upper sum..looking forwrd for ur rply.. tq..
Reply
- KK LEE on July 30, 2016 at 7:48 pm
  
  Solution will be updated soon
student on August 3, 2016 at 10:45 pm

Teacher , may i know what are the important point need to mentions in introduction ?
Reply
- KK LEE on August 3, 2016 at 10:51 pm
  
  Provides sufficient description to the given problem. (Upper sum. Lower sum) including the title.
- student on August 6, 2016 at 3:43 pm
  
  teacher can i have some example ? thank you
- KK LEE on September 6, 2016 at 11:41 pm
  
  Please check with your school teacher for details
TzeWin on August 7, 2016 at 12:36 am

hi mr.lee,our school have just started our maths M coursework.Thank you for the guidance eventhough i am not one of your students.
Reply
- paavitthira tamilchelvan on August 28, 2016 at 7:44 pm
  
  can u help me how to do it? becoz I don’t have any guideline to do it.
  tpaavitthira@gmail.com its my email. I hope u guys help me.
paavitthira tamilchelvan on August 28, 2016 at 7:40 pm

sir, I’m your student. I’m taking Maths M as my extra subject. So, I’m really confused how to coursework. can u help me?
Reply
- KK LEE on August 28, 2016 at 7:51 pm
  
  Which part? Did you get the handout in class?
- paavitthira tamilchelvan on September 1, 2016 at 12:08 am
  
  no I didn’t get any handout. they asked to me to it by own.
- KK LEE on September 1, 2016 at 2:49 pm
  
  You can get the handout from me in class tomorrow
- paavitthira tamilchelvan on September 1, 2016 at 10:28 pm
  
  okey sir. thank you.
Zy on August 29, 2016 at 9:44 pm

Hi Sir, can you please help me on introduction? I can’t find any example or description for it. What I got is only the definition of integration
Reply
- KK LEE on August 30, 2016 at 1:40 am
  
  https://www.google.com/?#q=upper+sum+and+lower+sum
- Zy on August 30, 2016 at 8:50 pm
  
  thank you sir 😀
yii on August 30, 2016 at 10:28 pm

hi, can u pls tell me what is the software u use to draw the graph??
thx a lot~
Reply
- KK LEE on September 6, 2016 at 11:37 pm
  
  Graph.
- KK LEE on September 6, 2016 at 11:38 pm
  
  http://www.padowan.dk
CY on September 16, 2016 at 12:25 pm

sir can i know to do the introduction and methodology??thx
Reply
- KK LEE on September 16, 2016 at 1:32 pm
  
  As mentioned above. Please refer to your teacher.
Sabar Rahman on September 23, 2016 at 3:10 pm

sir, may i know the title of this assignment?
Reply
wong.s.l on September 25, 2016 at 8:19 am

sir,I know how to do introduction and methology can you help me please
Reply
lim xin yan on September 27, 2016 at 12:40 am

How the 2(b) same with 2(a)(i) as 2(b) ci = a+(i-1) delta x?? Can you show me the step pls tq
Reply
- KK LEE on September 27, 2016 at 1:11 am
  
  Which part of 2b? I cant find the “same” part that u mentioned.
Nur on September 28, 2016 at 7:51 pm

Sir, may I know what do we need to write for the methodology?
Reply
Nurhazirah.M on February 6, 2017 at 1:36 pm

hai sir, may i know for term 2 assigment dont have ka?
Reply
- KK LEE on February 7, 2017 at 1:26 pm
  
  Ya. Not yet posted.
KX on April 10, 2017 at 11:51 am

Hi sir,may i know when do you post the asignment M term 2?
Reply
anthony on April 24, 2017 at 9:33 pm

Hello sir can I know when sem 2 assignment will be posted..?
Reply
- KK LEE on April 25, 2017 at 1:42 pm
  
  Hi there. I am not going to post it soon. Whatsapp me if you really need some help.
Manda on October 22, 2017 at 3:38 am

Hey , do you have math M stpm 2018 assignment? :))
Reply
- KK LEE on October 22, 2017 at 8:38 pm
  
  No