Introduction
The binomial theorem is a quick way of expanding a binomial expression that is raised to some power. When the binomial expressions are expanded, is there any type of pattern developing which might help us expand more quickly? It is fun to investigate how it works out in a pattern.
Sample Question
Question 1
(a) Expand for
.
(b) What observations can we make about the terms in the expansion of ?
(c) Write down the general formula for the binomial expansion of .
(d) Obtain the general formula for binomial expansion of where
is a rational number, and state the condition for the validity of the binomial expansion with a negative integral exponent or a rational exponent.
Question 2
Deduce the value of
(a)
(b)
Question 3
The number may be defined by
. Determine the approximate value for
.
Sample Solution
Question 1 (a)
Question 1 (b)
- There are
terms in the expansion.
- The first term’s powers start at
and go down.
- The second term’s powers start at 0 and go up.
- The coefficients are from Pascal’s triangle or
.
Question 1 (c)
Question 1 (d)
Question 2
Question 3
Here are our most recent updates posts
- Feel free to check it out -
STPM 2016 MT Functions Booklet A Page 5 Problem
Sample solutions of STPM 2016 Term 1 Mathematics Chapter 1 Functions A Problem Page 5
How to identify an iteration which is converges?
I received a Whatsapp message from student. He asked me whether the following shortcut is useful to determine whether the iteration is converges.
STPM 2015 Term 2 Mathematics State/School Trial Exam Papers
MBS added. If you have any of the papers, please submit all your school Mathematics (T) and Mathematics (M) trial exam papers and answers to me.
STPM 2015 Examination Timetable
Download all the STPM 2015 Term 1, Term 1 Ulangan, Term 2, Term 2 Ulangan, Term 3 and Term 3 Ulangan Examination Timetables.
STPM 2015 Mathematics (M) Term 2 Assignment
STPM 2015 Mathematics (M) Term 2 Assignment
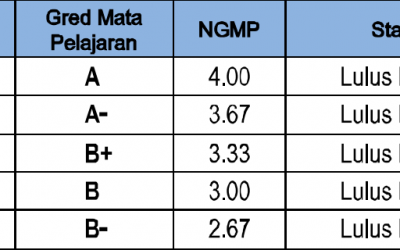
STPM 2014 Mathematics (T) and (M) Final Grade
STPM 2014 Mathematics Final Grade This is the collection of the final grade of the STPM Mathematics (T) and Mathematics (M) year 2014. The final grade of Mathematics (T) and (M) are based on the grade of Paper 1, Paper 2, Paper 3, and Paper 4(PBS). All the exam marks...





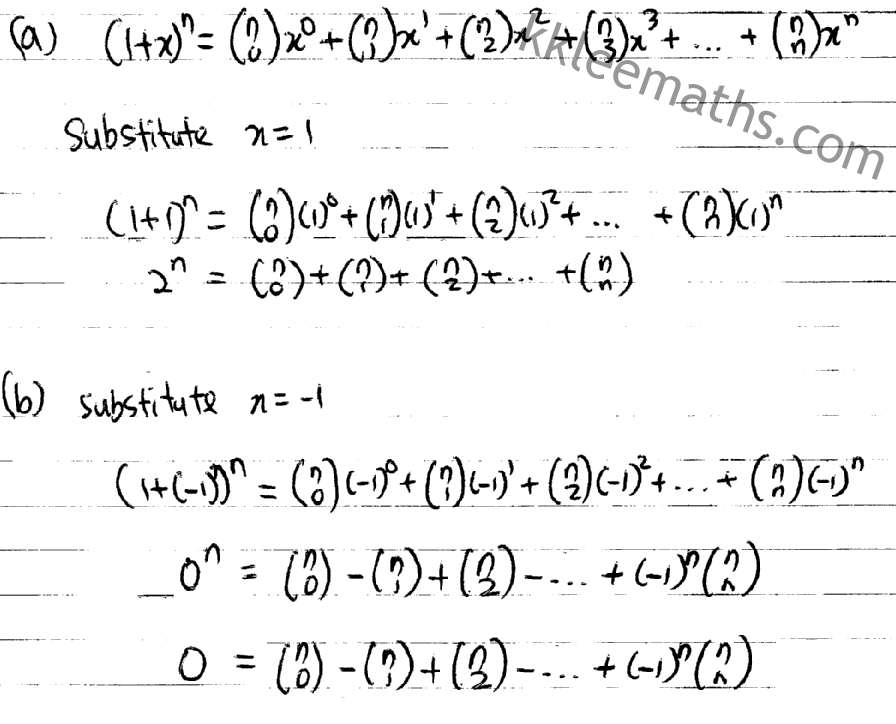





THX…
Sir, can u explain question 2
To get the equation, you need to substitute x=1 and x=-1
hi, may i know how to write the methodology? i have no idea. QAQ
For methodology, try to write about the methods/theorem/ways you used to solve the questions.
sir, may i know how to write about “communication”? and what is “viva”
It depends on your teacher.
How about term 2 methodology?
Hi. Are you referring to Mathematics (M)? I havent receive the question paper. T.T