Back to Blog

Read Article

Discussion –

175

Read Article

Discussion –

175

STPM PBS Assignment

STPM 2016 Mathematics (T) Term 1 Assignment

By KK LEE

July 29, 2015

STPM 2016 Term 1 Mathematics (T) Assignment

Introduction

Parametric equations express a set of related quantities as explicit functions of an independent variable, known as a parameter. An equation, relating variables x and y in Cartesian coordinates, can be expressed by parametric equations which describe a position on the curve.

Find information about parametric equations yourself.

Sample Question

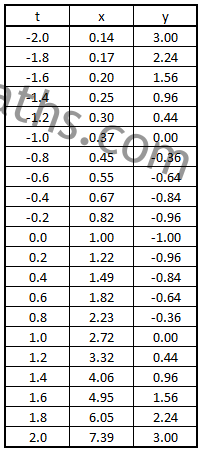
Parametric equations express a set of related quantities as explicit functions of an independent variable, known as a parameter. An equation, relating variables $x$ and $y$ in Cartesian coordinates, can be expressed by parametric equations which describe a position on the curve. 1 The parametric equations of a plane curve are defined by $x = e^t, y = t^2-1, -2 \leq t \leq 2$ . Tabulate the values $t$ , $x$ and $y$ , and plot the curve. 2 (a) Find three sets of parametric equations for the curve whose equation is $(y - 1)^2 = x - 49$ . (b) Is it possible to choose $x =-t^2$ as the parametric equation for $x$ ? Can you start with any choice for the parametric equation for $x$ ? (c) Can you start with any choice for the parametric equation for $y$ ? 3 Suppose that the position of a particle at time $t$ is given by

$x_1 = 2 \sin t, y_1 = 3 \cos t, 0\leq t\leq 2\pi$ ,

and the position of another particle is given by

$x_2 = \cos t - 2, y_2 = 1 + \sin t, 0 \leq t \leq 2\pi$ ,

(a) Sketch the paths of the particles on the same coordinate axes. (b) How many points of intersection are there? (c) Determine whether there is any point where the particles collide.

Sample Solution

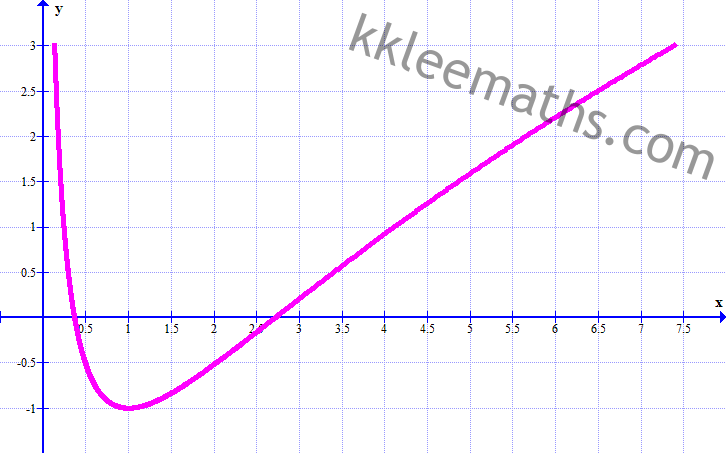
Scroll down for the sample solution 🙂 The solution below is sample solution and not the accurate answer. 🙂 Please refer to your school teacher if you want to get the correct answer.

Question 1

Question 2

(a) Three sets of parametric equations.

$x=t^2+49,y=t+1,t\in R$

$x=49\sec^2 \theta, y=7\tan\theta, \frac{\pi}{2}<\theta<\frac{\pi}{2}$

$x=4t^2+49, y=2t+1, t\in R$

Let me know if you know more.

(b) $x=-t^2$ is impossible to be chosen as the parametric equation for $x$ because $x-49$ must be always positive as $(y-1)^2 \geq 0$ for every values of $y$ . We can start with any choice for the parametric equation for $x$ as long as $x-49$ is not negative.

Question 3

(a) The curve in pink is $2\sin t, y=3\cos t$ . And the curve in black is $x=\cos t -2, y=1+\sin t$ .

(b) Based on the graph above, there are two points of intersection.

(c) To determine whether the particles collide, we need to solve the simultaneous equations from the parametric equations. Please remember the particles does not collide even you are able to solve the equations. You must verify the values. Collision happens only when positions are the same with same $t$ .

Verification

Hence, the particles collide at $t=\frac{3\pi}{2}$ .

Hence, the particles do not collide. Please do yourself for $y=0$ and $y=\frac{9}{5}$ . The particles collide at only 1 point.

Here are our most recent updates posts

- Feel free to check it out -

Old Syllabus STPM Book For Sale

STPM Reference

I am selling all the old STPM books for RM5 each. Please contact me if you are interested.

Complex Number Problem 1

KK LEE Booklet Solution

Here are our most recent updates posts- Feel free to check it out -

Pelangi MT Chapter 6 Revision Exercise Q17

Textbook Solution

The position vectors of point and relative to origin , are given by and...

MT Chapter 15 Booklet Page 23 Question 2

KK LEE Booklet Solution

Here are our most recent updates posts- Feel free to check it out -

Tags: Analytical Geometry MT Term 1 STPM 2016 STPM MT

← Previous Post Next Post →

KK LEE

KK LEE has been a STPM Mathematics tuition teacher since June 2006, but his love of Maths dates back to at least 1999 when he was Form 4. KK LEE started teaching in 2006 at Pusat Tuisyen Kasturi. He was known as "LK" when he was teaching in PTK. After teaching STPM Mathematics for 8 years in PTK, he joined Ai Tuition Centre in 2014. Over the years he has taught Mathematics (T), Mathematics (S), Mathematics (M), Additional Mathematics.

175 Comments

Fahmida on July 30, 2015 at 3:47 pm

Teacher may I ask a question…

Is number 2a) the equation for hyperbola or parabola…And if it’s hyperbola why is it so…
Thank you very much
Reply
- KK LEE on July 30, 2015 at 3:51 pm
  
  2a is parabola
- Fahmida on July 30, 2015 at 5:13 pm
  
  Thank you sir…I really appreciate it..
syah on August 1, 2015 at 11:11 am

Sir, I would like to ask on the equation x=e^t, did you eliminate the variable e or you just ignore it? If you eliminate it, how did you do it?
Reply
- KK LEE on August 1, 2015 at 12:50 pm
  
  Substitute the values of t into the equation of x
- WATUCARE on September 6, 2015 at 1:19 pm
  
  HUH IF I DO SO. THEN GOT 2 UNKNOWNS LOR.
jinnsern on August 3, 2015 at 4:17 pm

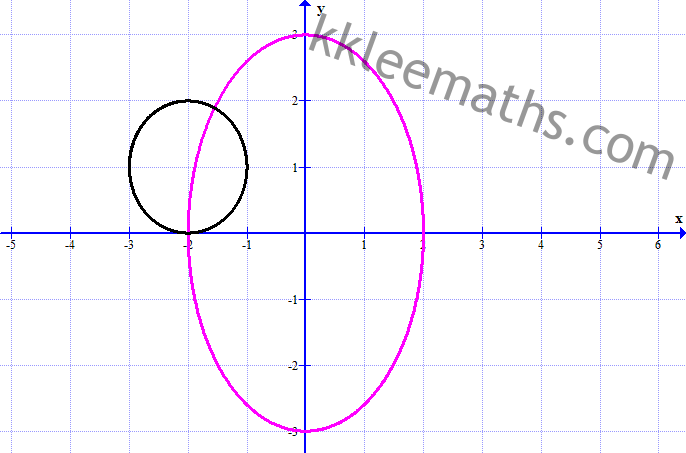
Teacher, how can i find the intersection points in 3(b)?
Reply
- KK LEE on August 4, 2015 at 10:36 am
  
  Question is asking “HOW MANY points of intersection”. So based on the graph, there are two points of intersection. DONE.
Hor cindy on August 3, 2015 at 5:02 pm

Sir, may i to ask you. how to get the 3 equation? i have no idea about this.
Reply
- KK LEE on August 4, 2015 at 10:37 am
  
  Any equations that satisfy the Cartesian equation.
ling ling on August 5, 2015 at 9:24 am

can i know how to get the third parametric equation for question 2a ?I tried so many times and still din get that ans….sir,can u give me some clues..
Reply
- KK LEE on August 5, 2015 at 9:51 am
  
  Refer the above comments, any parametric equations that satisfy the Cartesian equation given.
siaw ker on August 5, 2015 at 8:49 pm

can i know for the 2Qb)for the choice is based on the equation on the question 2a? ? thanks ^^
Reply
- KK LEE on August 5, 2015 at 9:21 pm
  
  No
- siaw ker on August 5, 2015 at 9:27 pm
  
  that means i can create my own parametric equation for x without links to the parabola equation for question2a) ?
- KK LEE on August 5, 2015 at 9:31 pm
  
  Question is asking can or not. And not asking what is the parametric equation. so if you are going to create your own. Ask your teacher and good luck.
Will Shong on August 7, 2015 at 12:20 am

Sir , can your kindly write the introduction , methodology and conclusion ? Thx a lot for your kindness
Reply
- KK LEE on August 7, 2015 at 12:52 am
  
  No
- will Shong on August 7, 2015 at 1:08 am
  
  Can you show me some guidance on doing the introduction , methodology and conclusion of this assignment .
- KK LEE on August 7, 2015 at 1:11 am
  
  Please ask your teacher. Different school teachers have different requirements
- Will Shong on August 7, 2015 at 1:23 am
  
  but teachers of my school just leave us to deal with it …. So I hope to get some information from you sir …
- KK LEE on August 7, 2015 at 10:22 am
  
  Hi. Sorry. Cant help on this. 🙂
Crist Ong on August 9, 2015 at 8:23 am

Sir…. for the parametric eqn right…. can this? :
1. y=sinϑ +1 ; x=50-(cosϑ)2 &
2. y=tanϑ +1 ; x=(secϑ)2-48……….
Reply
- KK LEE on August 9, 2015 at 11:53 pm
  
  yes. any equations
- Jack on September 7, 2015 at 9:45 am
  
  How you get that parametic eqn? steps?
- KK LEE on September 7, 2015 at 7:59 pm
  
  With the understanding of parametric equations, you can obtain the three equation easily.
iluvMathT on August 9, 2015 at 11:12 am

question 3C) on the verification part, after u sub the x value, why are they so many t value if use x=-6/5 but all prove it does not collide, but using x= -2 , many t value as well but only 1 prove it collide at that time. If t value we found prove it dont collide, then they are many t value outside which we dont find on the equation said it don collide.

question 3b)u sub x1 and x2 into sin^2 t +cos ^2 t = 1 and y value as well, and u found the point of intersection, but referring to the point we found on the graph , one of the point which is x=-6/5 does not seem to be logic, based on the graph it should -1.5 something, which clearly shown on the graph. does that mean it is wrong?
Reply
- KK LEE on August 9, 2015 at 11:58 pm
  
  For 3c. It is given that t lies between 0 and $latex 2\pi$.
  
  For 3b. I NEVER substitute any values in my calculation. Thanks
- iluvMathT on August 10, 2015 at 11:13 pm
  
  sry maybe i dont really understand, may i know for the first part of 3c), why do u sub x1/2 = sin t and x2 + 2 = cos t equation into sin^2 t + cos^2 t = 1?
- KK LEE on August 11, 2015 at 12:02 am
  
  To solve the simultaneous equations. You can use any other ways to solve the simultaneous equations to find the points where the particles collide.
- iluvMathT on August 13, 2015 at 12:36 am
  
  ok, so we found the point of intersection using simultaneous equations, which have two value for both x and y , but one of the x value which is x= -6/5 does not seem to be logic ,can u explain this?? because graphical method also can be used to find the point of intersection right? so if i use graphical method then my x coordinate for the point of intersection is not the same although y coordinate correct.
- KK LEE on August 13, 2015 at 12:57 am
  
  To find points of intersection of the curve and to find the point where the particles collide are not the same. Please ask your teacher or attend my class. 😛
- iluvMathT on August 13, 2015 at 1:28 am
  
  oic, then that makes clear that i dont really understand haha, cuz i thought u solve the simultaneous equation to find the point of intersection first, and assuming one of the particles be at that point then traces back t value and find coordinate of another particle.If x1=x2 and y1=y2 then it collide, So now your working is to find the point where particles collide? and may i know how to find point of intersection by using simultaneous equation?
- KK LEE on August 13, 2015 at 1:32 am
  
  Ways to find the points of intersection will only be shown to my students. Thanks
- iluvMathT on August 13, 2015 at 1:40 am
  
  haha alright then, tq so much for your time ! appreciate it !
Anson lee on August 11, 2015 at 12:41 pm

Is that q2 c is using b^2-4ac to solve ? And then we need to list up the possible parametric equation ?
Reply
- KK LEE on August 11, 2015 at 12:45 pm
  
  It depends on your teacher.
jessie kok on August 15, 2015 at 8:39 pm

Is there any other way to find the collision of points for 3(c) ?
Reply
- KK LEE on August 16, 2015 at 12:02 am
  
  There are many methods to find the points.
ng on August 17, 2015 at 7:06 pm

Question 2 how do start ? I don’t understand…
Reply
- KK LEE on August 17, 2015 at 7:33 pm
  
  Write the answer directly.
comfused on August 17, 2015 at 7:58 pm

Sir, are you sure that t= 3.785 & 5.690 when sin t= -0.6? When I use the calculator, I got a different answer.
Reply
- KK LEE on August 17, 2015 at 8:04 pm
  
  Yes. It is correct. Change your calculator or change your hand.
- MathsLover on August 19, 2015 at 8:11 pm
  
  Its correct. When you press your calculator,you shouldnt insert the negative in. Just insert the 0.6. After that you will get 36.8698… The negative sign shows that it’s actually in the third and fourth quadrant.For the third quadrant, its (180+36.8698), after that change the ans in term of rad. Which means you should take [(180+36.87)xπ]/180 = 3.786
  Do the same thing for the fourth quadrant (360-36.87) and you will get 5.64
  
  You’re welcome 🙂
- KK LEE on August 19, 2015 at 11:20 pm
  
  Haha.. A long explanation. But, u dint utilise the power of your calculator. 🙁
- yihui0225 on August 28, 2015 at 7:45 pm
  
  is 5.64 or 5.69？
- unknown on August 31, 2015 at 10:32 pm
  
  5.639 so it is 5.64
- MathsLoL on September 2, 2015 at 2:03 pm
  
  I have a different ans too..
lasini on August 20, 2015 at 8:58 pm

can we use graph(method)to solve ques 2
Reply
- KK LEE on August 20, 2015 at 10:51 pm
  
  Any methods. It depends on your teacher. 🙂
Tay on August 23, 2015 at 10:10 am

My teacher says that the answer for 2c is wrong.If you substitute your y equals to t² ,my graph will be limited to positive only.But according to the graph my y has negative values.
Reply
- KK LEE on August 23, 2015 at 12:53 pm
  
  Then u can adjust the answer yourself.
Aaron on August 23, 2015 at 3:15 pm

How to write a suitable title?
Reply
- KK LEE on August 23, 2015 at 11:09 pm
  
  “Race between turtle and rabbit using parametric equation”
- Wan Mai on August 26, 2015 at 6:16 pm
  
  Race between turtle and rabbit? is tht real?
- KK LEE on August 26, 2015 at 7:40 pm
  
  Why not?
- Wan Mai on August 26, 2015 at 7:41 pm
  
  excuse me, but anybody here have intro, methodology and others for this assignment? idk how to do.
  
  or sir, can you please write an entry abt how to write all this stuffs? thank you
- KK LEE on August 26, 2015 at 9:23 pm
  
  Cant help you on this.
nantha on August 26, 2015 at 11:23 am

Sir it seems that there is more than 1 graph fr various valuess of t
Reply
- KK LEE on August 26, 2015 at 7:39 pm
  
  What you mean?
AH BENG on August 27, 2015 at 1:54 pm

Sir,Mat i know how to do the intro??
Reply
- KK LEE on August 27, 2015 at 3:56 pm
  
  Please ask your school teacher.
Kok on August 28, 2015 at 2:02 am

Sir for the question 3c
I think you made a mistake
Its 5x^2 + 16x + 15
Not 5x^2 + 16x + 12
Reply
- Kok on August 28, 2015 at 2:26 am
  
  Eh sorry correct already
- yihui0225 on August 28, 2015 at 7:35 pm
  
  I think 5x^2+16x+12 is correct.
yihui0225 on August 28, 2015 at 7:52 pm

Hello sir. How to calculate the position of both particles collide in Q3 c）when t=3.785 and 5.640?
Reply
- KK LEE on August 28, 2015 at 11:25 pm
  
  Subs into the equation of x and y
- yihui0225 on August 30, 2015 at 10:33 pm
  
  Which equation of x and y？
- KK LEE on August 31, 2015 at 12:20 pm
  
  Please refer to the question. It is stated there
Ivan on August 29, 2015 at 11:49 am

Sir, how do i explain the part for 3(c) in my methodology, whereby i change the sin^-1(-0.6) to 3.785 and 5.64?
Reply
- KK LEE on August 29, 2015 at 5:14 pm
  
  “By calculator”
Yong Sheng on August 29, 2015 at 11:00 pm

Sir….. Regarding no.2(a) … If I let x=t^2 , y=+-(surd t^2-49)+1…. In this case, I’ll have 3 parametric equations. One x and two y. So which of the y parametric eqn should I choose to get a set??
Reply
- KK LEE on August 29, 2015 at 11:06 pm
  
  Please change to others. Unless this is your teacher’s requirement
Ain canti on August 31, 2015 at 1:23 pm

Sir , how to find three sets of parametric equation like question 2a ?
Reply
- KK LEE on August 31, 2015 at 1:27 pm
  
  Any equations that satisfy the Cartesian equation
KHZ on August 31, 2015 at 1:31 pm

Sir,may i ask y did u chg the ans to rad when using x=-6/5 in verification step…thx in advance
Reply
- KK LEE on August 31, 2015 at 5:45 pm
  
  It is in radian from the beginning. I dint change anything.
- KHZ on August 31, 2015 at 10:44 pm
  
  ops, sry my bad
Catherine on August 31, 2015 at 10:42 pm

Sir,at verification step, if i substitute x=-2 into x=cos t – 2, then cos t would be 0 and i will get 2 answers, so i just have to conclude that the particles would not collide when t=pi or is it that i am only supposed to use x=2sin t
Reply
- KK LEE on August 31, 2015 at 11:58 pm
  
  Use ALL equations to verify.
unknown on September 1, 2015 at 9:50 pm

sir, do you have any example or tips on how to do the methodology and conclusion?
Reply
- KK LEE on September 1, 2015 at 10:42 pm
  
  Nope
WRN on September 1, 2015 at 11:43 pm

Sir, why the 2nd parametric equation in 2(a)is y=7tanθ, but not y=7tanθ+1? I thought it should be y=7tanθ+1…
Reply
- KK LEE on September 1, 2015 at 11:59 pm
  
  Yes. Please edit yourself.
- MathsLoL on September 2, 2015 at 1:39 pm
  
  May I know How do you find the parametric eqn for y=7tan + 1 ??
- KK LEE on September 2, 2015 at 11:54 pm
  
  Make sure you can get all the points.
nabilah on September 6, 2015 at 12:23 pm

sir…may i ask you one quest…for the answer of Q2 n Q3…should i write on methodology or results?
Reply
- KK LEE on September 6, 2015 at 7:45 pm
  
  result
nabilah on September 6, 2015 at 12:38 pm

another quest,,,,,where did you get t=3/2 pi….for Q3(c) verification,,,,when i press on the calculator,,,the answer is diffrence from yours
waiting for your explanation
Reply
- KK LEE on September 6, 2015 at 7:46 pm
  
  Make sure you are using the rad mode. Else change your calculator.
MICHAEL on September 8, 2015 at 10:23 pm

sir, i notice sumthing…… according to u….
when x=-6/5 the 2nd t= 5.690
but t=5.640 when u are relating the t to both curves……
i already tried using calculator…. t=5.640 is more reasonable……
Reply
- KK LEE on September 9, 2015 at 12:45 am
  
  I cannot understand what you asking. I hope you have solved your question.
aaron on September 10, 2015 at 8:19 pm

sir,how to do the methodology for those question?
Reply
- KK LEE on September 11, 2015 at 1:49 am
  
  Please refer to your school teacher. Thanks
nabilah on September 10, 2015 at 8:49 pm

sir,,,why did you used sin^2t-cos^2t=1 for quest 3 C).
why did you used alphbet t??can we use any aplphbets other than t?
Reply
- KK LEE on September 11, 2015 at 1:50 am
  
  Because there is t in the question.
- nabilah on September 11, 2015 at 1:15 pm
  
  thanks a lot sir
nabilah on September 12, 2015 at 10:46 am

sir,may i know,,where did you get the coordinates for question 3 C)?did you subsitute the values of t in the equation of x=2sint,x=cost-2,y=3cost,y=1+sint?
Reply
- KK LEE on September 14, 2015 at 7:55 pm
  
  yes
Mariani on September 14, 2015 at 8:58 pm

Sry sir…it’s tht can,if I just gv the definition of parametric equ n some example for intro.^^
Reply
- KK LEE on September 15, 2015 at 1:21 am
  
  Ya. It depends on your teacher.
ila on September 15, 2015 at 7:27 pm

sir can i know how to do the conclusion. what point must we put in the conclusion
Reply
- KK LEE on September 15, 2015 at 7:30 pm
  
  Hi. Please ask your teacher. I am not going to help in this part.
- Ila on September 16, 2015 at 10:44 pm
  
  Thank you sir. Sir why x-49 must be in positive?
- KK LEE on September 16, 2015 at 10:58 pm
  
  Because $latex \sqrt(x-49)$ is defined only if $latex x-49>=0$.
Nantini on September 16, 2015 at 2:00 pm

Sir , can i know how to draw the graph using computer
Reply
- KK LEE on September 16, 2015 at 4:56 pm
  
  Sorry. I cant teach here. Please youtube yourself.
KHZ on September 16, 2015 at 9:48 pm

Sir, does t represent the time when the particles collide?
Reply
- KK LEE on September 16, 2015 at 10:11 pm
  
  t represents the time, any time when the particle is moving
- KHZ on September 16, 2015 at 10:12 pm
  
  kk, tq sir
James on September 17, 2015 at 4:15 pm

Sir, can give me some idea how to write the title
Reply
a on September 17, 2015 at 9:04 pm

Sir can i know how to find the range of the second for question 2(a)?
Reply
- KK LEE on September 18, 2015 at 12:56 am
  
  You have to test one by one to get the complete curve.
Cukudut on September 18, 2015 at 12:38 pm

Sir what means of this “$latex \sqrt(x-49)$ is defined only if $latex x-49>=0$.”
Reply
- KK LEE on September 18, 2015 at 6:06 pm
  
  x-49 must be positive, else the square root function cannot be defined.
BKHong on September 20, 2015 at 2:00 am

For question 3c, x=-6/5 and -2,then to find t,I have to use equation x=2sin t right?Should I use another equation of x ,(x=cos t-2)to find t?
Reply
- KK LEE on September 20, 2015 at 10:02 pm
  
  You can use any equations.
Jason Chin on September 21, 2015 at 9:12 pm

For the 2a) question right, x= 4t^2+49 y= 4t+1
Sir am i right?
Reply
- KK LEE on September 21, 2015 at 11:43 pm
  
  x= 4t^2+49 y= 2t+1
- Jason Chin on September 27, 2015 at 12:58 am
  
  NO sir. i mean x= (4t)^2+49 y= 4t+1
  So sir. am i right?
- KK LEE on September 27, 2015 at 1:11 am
  
  can
dayang on September 21, 2015 at 10:22 pm

sir, for the question 2a) can i just substitute the x=e^t into the eq 2a as my parametric equation?
Reply
- KK LEE on September 21, 2015 at 11:44 pm
  
  Can. If you can find the corresponding y
rickywong on September 22, 2015 at 2:20 pm

Teacher,can you tell me how to get 3 parametric equation in 2a.please?
Reply
chalester on September 22, 2015 at 8:55 pm

Teacher,can you give me same tips on how to write methology and conclusion because our maths t teacher already retire and want to wait until next year new teacher come and we don’t have any teacher guide us.Thanks you for your reply~
Reply
- KK LEE on September 22, 2015 at 11:50 pm
  
  For methodology, try to write about the methods/theorem/ways you used to solve the questions.
  
  For conclusion, you can rewrite again all your important result from each part and write one or two example that related.
rickywong on September 22, 2015 at 9:11 pm

Sir,can you tell me how to get 3 parametric equation in Q2a,thx.
Reply
- KK LEE on September 22, 2015 at 11:53 pm
  
  It can be obtained directly if you know what is parametric equation. I can’t explain further here.
xxxxxxxxx on September 22, 2015 at 11:52 pm

Hi ?I want to ask that the questions 2)a) are we need to form 3 parametric equation form that cartesian equation or just sub the x or y value that you give into that cartesian equation??? Thank you ?
Reply
- KK LEE on September 22, 2015 at 11:55 pm
  
  You need to form 3 equations.
- xxxxxxxxx on September 23, 2015 at 12:04 am
  
  Ok, thank you very much.
Chalester on September 23, 2015 at 7:47 pm

thank you for your reply(^_^)
Reply
Sharon on September 24, 2015 at 11:17 am

Sir, for question 2 a) can I let x=t, x=2t and x=t^2 and in each case express y in terms of t. [x=t, y=+/- square root(x-49)-1] is a set?
Reply
- KK LEE on September 24, 2015 at 12:53 pm
  
  For me, No. For your teacher, i don’t know.
Hedarus on September 24, 2015 at 6:37 pm

Can i use y=t,y=(t^2)-1 and y=-t^2 to prove that it can used for y in 2(c)?
As my teacher want us to show the equation….
Reply
- KK LEE on September 25, 2015 at 1:19 am
  
  Can. If your teacher accept.
Hi on September 24, 2015 at 11:37 pm

Sir,what should i write for an introduction for parametric equation?
Reply
- KK LEE on September 25, 2015 at 1:18 am
  
  Hi. It depends on your teacher. Please google for some related info and use it.
ying on September 25, 2015 at 2:23 pm

Sir, is it 2(a) need to plot the curve??because the question have say “….the curve whose equation is…..” so need to sketh a parabola graph or not??
Reply
OnnGusta on September 26, 2015 at 2:30 pm

hi sir , 🙂 can i ask about question 2(b) why cannnot ?
Reply
- KK LEE on September 27, 2015 at 12:33 am
  
  Hi. Reason is stated there.
MTPhobia on September 27, 2015 at 8:05 pm

Sir,for question 2(a),How to find the other 2 sets of parametric equations?For set 1,I used the formula x=at^2 and y=2at…but how about the other 2 sets?How can i get the other 2 sets?I have no idea…Just use back the same formula or there is another way to solve this?
Reply
- MTPhobia on September 27, 2015 at 9:20 pm
  
  Does it mean any parametric equations of curve as long as it satisfy the Cartesian equation?So,If that is true,can I use the parametric equation of hyperbola?
- KK LEE on September 27, 2015 at 9:57 pm
  
  You can use any equation that satisfy the original equation.
- MTPhobia on September 27, 2015 at 10:06 pm
  
  How to meant by satisfy the original equation?
- MTPhobia on September 27, 2015 at 10:17 pm
  
  Ohh…I think maybe i get what you mean…Thanks a lot!
Zoe on September 28, 2015 at 12:25 am

Hi Sir, to find if the particles collide in 3c, can I do a table of t(0, pi/2, pi, 3pi/2, 2pi values), x1, x2, y1 & y2? and subs t values into the original equations in the questions to find the (x,y)coordinates that are the same? The answer will still be 3pi/2 as point where they collide.
Reply
- KK LEE on September 28, 2015 at 7:45 pm
  
  For me, NO. For your teacher, i don’t know.
Alexa A. on September 29, 2015 at 8:35 pm

Can you explain more from 3.C Verification? Only subs the value of x on x= 2 sin t?
Reply
- KK LEE on September 30, 2015 at 12:55 am
  
  Substitute into all the original equations to verify
Drake on October 3, 2015 at 2:30 pm

Hi sir, may i know that for the question 3, should i use the same value as you had used for the simultaneous equation and verification or should i use a different set of values?
Reply
- KK LEE on October 3, 2015 at 11:20 pm
  
  Same
Lim on October 11, 2015 at 7:45 pm

Hello, sir. How do I get the values of t for Q3?
Reply
- KK LEE on October 13, 2015 at 12:37 am
  
  Solve the simultaneous equations
yyee on October 17, 2015 at 12:09 am

2a can use standard form of parabola to create the equation?
Reply
- KK LEE on October 18, 2015 at 10:05 pm
  
  For me NO. For your teacher i dont know
everyone on October 17, 2015 at 6:12 pm

that helps alot.thanks
Reply
..... on October 20, 2015 at 5:09 pm

Sir, can you please give me some example of the application of parametric equation in our daily life??? Because I cannot find it in the internet……..
Reply
- KK LEE on October 29, 2015 at 11:17 pm
  
  https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=0CB0QFjAAahUKEwi1ur37_OfIAhXmFqYKHfIcCpc&url=http%3A%2F%2Fwww.ck12.org%2Fbook%2FCK-12-Precalculus-Concepts%2Fsection%2F10.5%2F&usg=AFQjCNGytl0OlsdzRNpXqRXax-NJf4J63Q&sig2=b6hSEQXULOydzgFfMTqJGg
random on October 23, 2015 at 11:27 pm

Hi sir
For 2a
Can I use x=50-sin^2€ and y=cos€+1 and the range of € is between 0 and pi?
I have calculated the values using the range but it seems to be a graph with y-axis as major axis but the other two equations above are graphs with x-axis as major axis..
Reply
- KK LEE on October 29, 2015 at 11:15 pm
  
  You can try to switch the x and y
Smaster on October 26, 2015 at 4:01 pm

Sir,may I know how to get 3.785 and 5.640 when x=-1.2
Reply
- KK LEE on October 29, 2015 at 11:15 pm
  
  Using calculator
Wei on October 29, 2015 at 10:46 pm

Sir , for x=-2 and y=0 , I’ve got the value of t that is (3π/2) , so is it that the coordinates of the ellipse and circle for x=-2 AND y=0 are the same ?
Your student here hahahahaha
Reply
- KK LEE on October 29, 2015 at 11:08 pm
  
  Yes
Alex on November 3, 2015 at 10:33 pm

Sir,how to write the conclusion and methodology?
Reply
Josephine on November 25, 2015 at 6:44 pm

Excuse me teacher? I would like to ask about what should i write for any comment or statement after i plot the curve(question 1)?Can you guide me some suggestions?
Reply
- KK LEE on November 25, 2015 at 11:23 pm
  
  You can explain the shape.
Kim on December 3, 2015 at 4:15 pm

sir for question 2a ,may i make the original equation into this form ? x²/36² – y²/6² = 1 ? thn my parametric eqaution will be like this,x = 36 sec ,y = 6 tan
Reply
- KK LEE on December 5, 2015 at 9:32 am
  
  For 2a. It is a parabola, which means it cant be x²/36² – y²/6² = 1
Damn on December 11, 2015 at 7:34 pm

u know what , u r rude, n i read all your replies to all the comments.. u kinda reply in a sarcastic way.. just chill on , cause we r new to this kinda no guide assignment.. we need some help bcoz all of our school teacher dont give a damn.. so the point is have some courtesy to share knowledge… hope u get me, stingy 🙂
Reply
- KK LEE on December 12, 2015 at 12:34 am
  
  All right. Thanks of your comment.
  
  1. I am not a school teacher. And i never attend any meeting regarding the assignment. So do not expect me to know all the school teachers requirement. I have tried my best to give the information that i know. I have students from different schools. That’s why i know different school teachers have different requirement on the particular questions. This is also the reason i never answer all the questions that are not related to maths.
  
  2. I am posting all maths related solutions for your reference and please do not expect me to post 100% answers.
  
  3. I have tried my best to help and this will be my last posting on solutions of assignments. Thanks.
- Rx on April 9, 2016 at 7:31 am
  
  U r so disgusting u know?people give u a sample to refer,u never say tanks, determine, but u still complain that the ans is not acceptable in your school?so ridiculous,no one is a must to provide amethyst is needed by your teacher,ok???I feel pity on u….
Jack on March 17, 2016 at 8:33 pm

sir, do you have math (T) TERM 2 assignment solution?
Reply
- KK LEE on March 17, 2016 at 8:43 pm
  
  Hi. You can refer to this post.
  
  https://kkleemaths.com/stpm-pbs-assignment/stpm-2016-mathematics-t-term-2-assignment/