Trigonometry
Transformation
A function is a relation whereby every input gives a unique (exactly one) output. There are four
possible ways to represent a function; verbally, numerically, visually and algebraically.

2. Give at least five different representations of a simple discrete function.
3. Give at least three different representations of a continuous function.
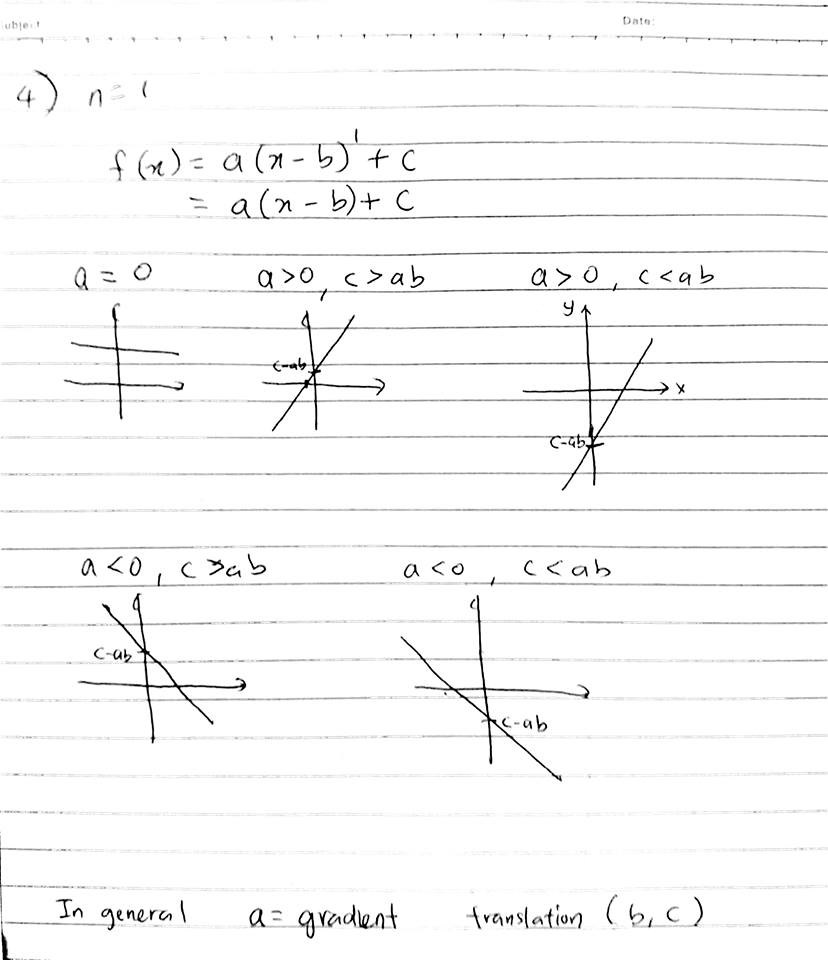
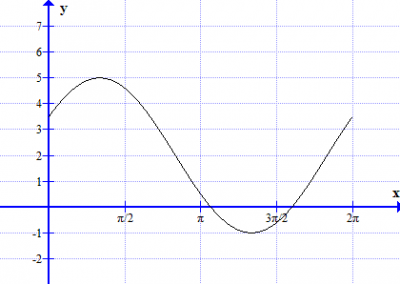
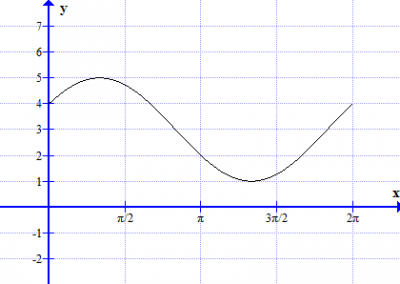
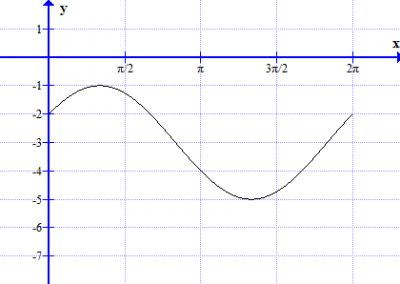
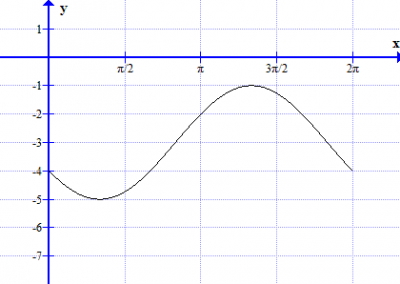
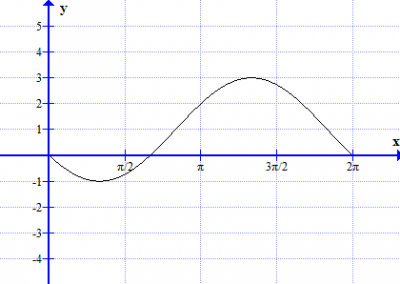
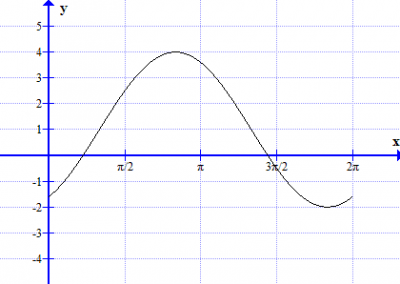
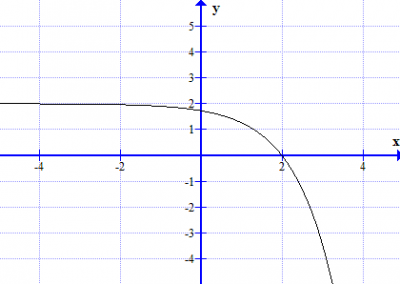
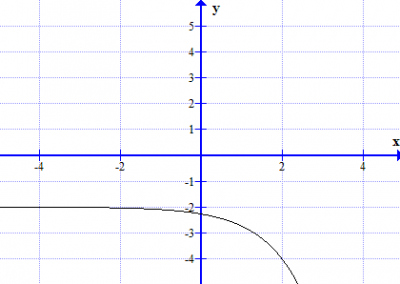
Describe, with sketch graphs, the function f for different values of a, b and c for n = 1,2 and 3.
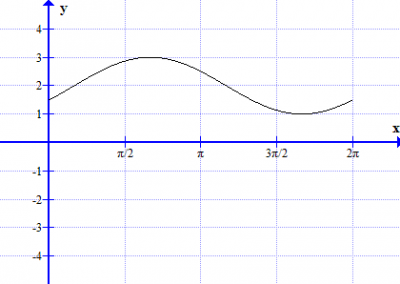
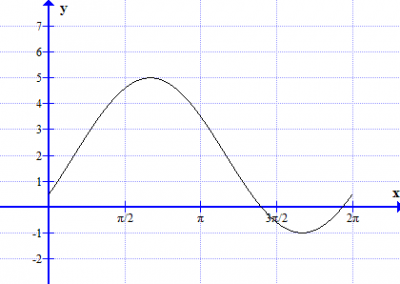
5 Repeat task 4 with the trigonometric function
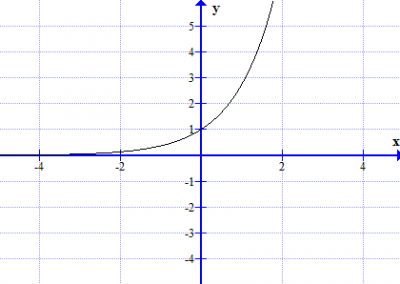
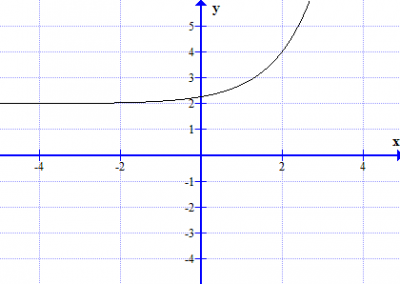
6 Repeat task 4 with an exponential or logarithmic function of your own choice.
For question 1. Please google for the definition.
For question 2. You can assign any functions but make sure your range is “integer”.
For question 3. You also can assign any functions but make sure your range is “any numbers”.
For n=1. Some ideas for you. You can try a>0, a=0, a<0, b>0, b=0, b<0, c>0, c=0, c<0. So you will get many combinations. For the total number of combinations, please refer to your school teacher.
For n=2. Same.
For n=3. Same.
I am not going to sketch the graph for n=3. Please do it yourself. Thanks.
For n=1. Some ideas for you. You can try a>0, a<0, a>c, c>a, b>0, b<0, b in first/2nd/3rd/4th quadrant. So you will get many combinations. For the total number of combinations, please refer to your school teacher.
In short. a is amplitude. b translation (left/right). c is translation (up/down).
For n=2. Same.
For n=3. Same.
I am not going to sketch the graph for n=2(frequency=2) and 3(frequency=3). Please do it yourself. Thanks.
You can consider
For n=1. Some ideas for you. You can try a>0, a<0, b>0, b<0, b>0, c<0, c>0. So you will get many combinations. For the total number of combinations, please refer to your school teacher.
In short. a is scale factor(vertical). n is scale factor(horizontal). b translation (left/right). c is translation (up/down).
Here are our most recent updates posts
- Feel free to check it out -
STPM 2015 MT Differentiation Booklet A Page 19 Problem 9 Question 12
STPM 2015 Term 2 Mathematics (T) Chapter 8 Booklet Differentiation A Page 19 Problem 9 Question 12 Solution
STPM 2015 MT Chapter 9 Booklet A Page 10 Problem 7 8 9
STPM 2015 Term 2 Mathematics (T) Chapter 9 Booklet integration A Page 10 Problem 7 Problem 8 Problem 9 Solution
STPM 2015 Term 1 Result Day
STPM 2015 Term 1 Result Day
STPM 2015 Mathematics (T) Term 2 Assignment
Answer and Solutions of STPM 2015 Term 2 Maths (T) Assignment
STPM 2014 Ulangan Result Day
STPM 2014 Repeat Term 1 and Term 2 Result Day
Geometric Progression I
Geometric Progression I




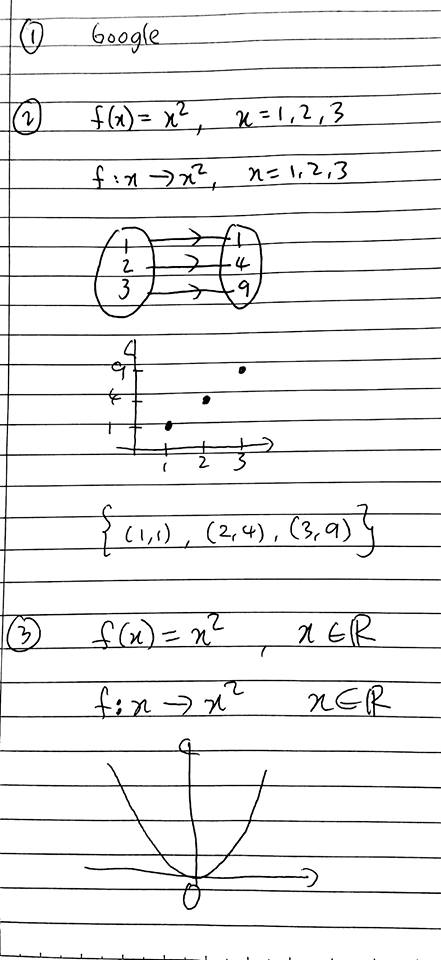











sir,hope u can upload the solution faster,thank u
After my holiday
Sir, I need the solution before the holiday ends as it is the deadline for my school.
Sample solution will be posted when they are available or after i discuss the solution in class.
for question 5? thanks
Sample solution will be posted when they are available or after i discuss the solution in class.
How about Question No.6?
how to do question no.6
Solution will be posted only when they are available
Sir
My school teacher she won’t discuss any introduction, methodology and conclusion for our coursework.
Could you at least give some guidance on how to write those things??
Thank you
halo
Thank you sir, help me a lot. But hope u can upload the solution faster
The solution is complete now
sir , for question 6 just do n=1 only?
No. You should do for n=2 and also n=3.
Can i know how to write for introduction, methodology and conclusion?
sir, how to explain the graph after sketching in question 4?
Parabola shape with transformations
What is the function formula for the logaritma no.6… I need to know…u just show it for exponential…
Do we have to write a small conclusion for every graph that is drawn?
It depends on your teacher.
sir,can you give me some guides for the introductions and methodology please?
As mentioned above. Please refer to your teacher.
Can i know the website you are using to plot the graph?
Graph. You can download from padowan.dk
Sir may i know do we need to put a value in question 3? Because x is equal to all real number.
sir, can help for methodology?
how i can do question four using microsoft excel. my teacher told us to plot the graph using microsoft excel.
You can use the graph function in the excel. Youtube might help you.
ive tried excel for my graphs however it was to no avail because u cant get a graph just by keying in the equation with your chosen values of a b and c. U will need to key in the x-values which is painstakingly time consuming. The beauty of online generated graphs, the equation itself gives u a graph given that u have ur a b and c values. Screenshot and crop or use snipping tool to get the graph on microsoft words and arrange according to your liking. I hope your teacher is not insisting that u use excel and excel only…
sir, what do you mean by the scale factor for exponential graphs? when n increases, does the scale factor decrease?
sir, can you help us for the introduction, methodology, and conclusion. my teacher wont help us.
Hi, thanks for sharing.
Can you guide me how to do Term 2 assignment 2017?
Hello sir
Thanks for the sem 1 guidence. Will sir provide some guidence for the semester 2 project work
Yes